Paralelepípedo retângulo
Seja o paralelepípedo retângulo de dimensões a, b e c da figura:
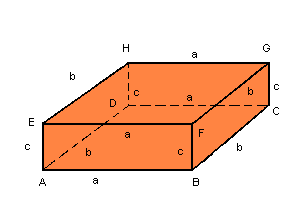
Temos quatro arestas de medida a, quatro arestas de medida b e quatro arestas de medida c; as arestas indicadas pela mesma letra são paralelas.
Diagonais da base e do paralelepípedo
Considere a figura a seguir:
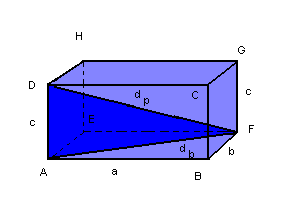 |
db = diagonal da base
dp = diagonal do paralelepípedo
|
Na base ABFE, temos:
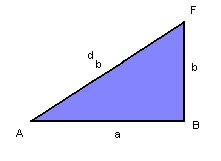 |
No triângulo AFD, temos:
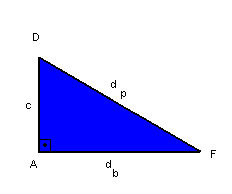 |
Área lateral
Sendo AL a área lateral de um paralelepípedo retângulo, temos:
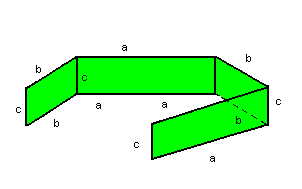
AL= ac + bc + ac + bc = 2ac + 2bc =AL = 2(ac + bc)
Área total
Planificando o paralelepípedo, verificamos que a área total é a soma das áreas de cada par de faces opostas:
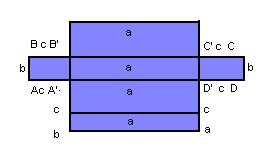 |
AT= 2( ab + ac + bc)
|
Volume
Por definição, unidade de volume é um cubo de aresta 1. Assim, considerando um paralelepípedo de dimensões 4, 2 e 2, podemos decompô-lo em 4 . 2 . 2 cubos de aresta 1:
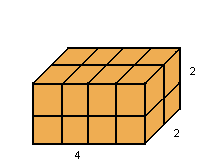
Então, o volume de um paralelepípedo retângulo de dimensões a, b e c é dado por:
V = abc
Como o produto de duas dimensões resulta sempre na área de uma face e como qualquer face pode ser considerada como base, podemos dizer que o volume do paralelepípedo retângulo é o produto da área da base AB pela medida da altura h:
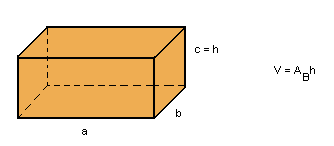
Fonte: www.somatematica.com.br/
Questões resolvidas de vestibulares sobre paralelepípedo
1) As medidas das arestas de um paralelepípedo retângulo são proporcionais a 2, 3 e 4. Se sua diagonal mede 2√29 cm, seu volume, em centímetros cúbicos, é:
a) 24
b) 24√29
c) 116
d) 164
e) 192
Solução:

2) Um armário, com a forma de um paralelepípedo de dimensões 0,5m, 2,5m e 4m, deve ser pintado. O rendimento da tinta empregada é de 5m² por litro. Determine a quantidade de tinta necessária para pintar toda a parte interna do armário.
Solução:
Calculando a área total, temos: .
At = 2x{(0,5)(2,5)+(0,5)(4)+(2,5)(4)} = 26,5m²
Logo, empregando 5m² por litro, serão gastos 26,5/5= 5,3 litros.
At = 2x{(0,5)(2,5)+(0,5)(4)+(2,5)(4)} = 26,5m²
Logo, empregando 5m² por litro, serão gastos 26,5/5= 5,3 litros.
3) A garagem subterrânea de um edifício tem 18 boxes retangulares, cada um com 3,5m de largura e 5m de comprimento. O piso da garagem é de concreto e tem 20cm de espessura. Calcule o volume de concreto utilizado para o piso da garagem.
Solução:
O piso terá a forma de um paralelepípedo muito fino, já que sua espessura é de 0,20m. Esse piso entrará em cada box. O volume de cada piso é V = (3,5) x (5) x (0,20) = 3,5m3. O volume total utilizado nos 18 boxes será V = (18) x (3,5) = 63m³.
4) Dispondo-se de uma folha de cartolina, de 70cm de comprimento por 50cm de largura, pode – se construir uma caixa, sem tampa, cortando-se um quadrado de 8cm de lado em cada lado. Determine o volume desta caixa.
O desenho mostra a parte retirada de cada lado e a caixa construída na forma de um paralelepípedo.
O volume será V = (54) x (34) x (8) = 14688cm³.
5) O volume de um paralelepípedo retângulo é 1620 m³. Calcular as arestas sabendo que estas são proporcionais aos números 3, 4 e 5.
a/3 = b/4 = c/5 = K
a = 3k
b = 4k
c = 5k
V = a * b * c
1620 = a * b * c
1620 = 3k * 4K * 5K
60k³ = 1620
k³ = 27
K = 3
temos, então: a = 9, b = 12 e c = 15
6) ( Unirio ) Um engenheiro vai projetar uma piscina, em forma deparalelepípedo retângulo, cujas medidas internas são, em m, expressas por x, 20 – x e 2.

O maior volume que esta piscina poderá ter, em metros cúbicos, é igual a:
a) 240
b) 220
c) 200
d) 150
e) 100
Solução:
Vamos entender o problema:
O volume de um paralelepípedo retângulo é dado pelo produto de suas 3 dimensões, ou seja, C x L x A, onde C de comprimento, L de largura e A de altura.
Do enunciado do problema podemos escrever:

Que é uma função do 2° grau, cujo volume está em função de x. Como a concavidade está voltada para baixo, logo apresenta valor de Máximo, justamente o que estamos procurando.
Resolvendo a Equação do 2° grau:

Encontramos as raízes da equação do 2° grau que indicam onde o Volume de nossa piscina vale 0.
Aqui vale um comentário: Apesar de não ter sido pedido no Exercício vamos construir o Gráfico de Volume em função de x. Um vez que estamos trabalhando com medidas, as mesmas não podem ser negativas, logo o nosso gráfico ficará limitado a imagens maiores ou iguais a zero e seu domínio compreendido entre as raízes.

Podemos lembrar que estamos procurando o maior volume, e para isso precisamos das coordenadas do vértice de uma parábola. Podemos nos lembrar das coordenadas:

Porém, das características de uma função do 2° grau, sabemos que a mesma apresenta um eixo de simetria e do gráfico podemos observar que:

Logo:

Portanto para x = 10 m, temos nossa piscina com Volume máximo de 200 metros cúbicos.
Alternativa C.
E a piscina ficaria com as medidas de 10m x 10m x 2m.
7) (PUC-RIO) Um paralelepípedo de dimensões 0,10 m x 1,00 m x 0,10 m flutua numa piscina profunda. A densidade do material do qual é feito o paralelepípedo é ρ = 800 kg/m3. Supondo que a densidade da água é ρagua = 1000 kg/m3, g = 10 m/s2 e que o paralelepípedo está flutuando em equilíbrio estático, calcule o volume do paralelepípedo
Solução:
O volume sob a linha d´água V D = F E / (ρagua g) = 80 /(1000 x 10) = 8 x 10-3 m3 = 8 Litros.
a) 0,066
b) 0,072
c) 0,096
d) 0,600
e) 1,000
b) 0,072
c) 0,096
d) 0,600
e) 1,000
Solução:
Volume Vi do indivíduo corresponde ao volume do líquido deslocado, que é o volume de um paralelepípedo retângulo de altura h e de área de base 0,8 . 1,2.
Então, Vi = 0,8 . 1,2 . 0,075.
Resposta: alternativa b.
Logo, Vi = 0,072 m³
9) Um vaso tem a forma de um paralelepípedo retângulo com base quadrada de diagonal igual 15Ö 2 cm e altura 8 cm.
A capacidade desse vaso, em litros, é:(01)1,2
(02) 1,5
(03) 1,8
(04) 12
(05) 18
SOLUÇÃO:
O comprimento D da diagonal de um quadrado de lado L é dado por:
D = L.Ö 2 . Portanto, vem: 15Ö 2 = L.Ö 2 \ L = 15 cm
O volume do paralelepípedo retângulo de base quadrada, será dado por:
V = Sb . h
Onde Sb = L2 = 152 = 225 cm2 (área da base quadrada).
Portanto V = 225cm2 . 8cm = 1800 cm3
E como 1 litro = 1000 cm3, teremos V = 1,8 litros.
A resposta correta é a de número (03).
Solução:
O paralelepípedo formado pelos cubos de 1 cm de aresta (1cm3) que ficarão sem cobertura terá um volume menor:
V = (5-2) cm × (6-2) cm × (7-2) cm = 3 cm × 4 cm × 5 cm = 60 cm3. Assim, o valor procurado será de 60 cubos.
11) Uma fábrica produz barras de chocolates no formato de paralelepípedos e de cubos, com o mesmo volume. As arestas da barra de chocolate no formato de
paralelepípedo medem 3 cm de largura, 18 cm de comprimento e 4 cm de espessura. Analisando as características das figuras geométricas descritas, a medida das arestas dos chocolates que têm o formato de cubo é igual a
a) 5 cm. b) 6 cm. c) 12 cm. d) 24 cm. e) 25 cm.
Solução:
Sendo Vp e Vc os volumes das barras de chocolate de formato “paralelepípedo” e “cubo”, respectivamente, e sendo a a medida da aresta do cubo, temos:

12) (ENEM-2006)

SOLUÇÃO:
Interpretando a vazão como a razão entre o volume de água e o intervalo de tempo para o escoamento desse volume, poderemos aplicar a regra de três para obter o tempo gasto necessário para o nível de água baixar do ponto máximo até a jusante.
O primeiro passo para esse cálculo é identificar o volume de água no formato de um paralelepípedo com altura de 20 m, comprimento de 200 m e largura de 17 m:
Como a vazão é de 4.200 metros cúbicos por minuto, com a regra de três calculamos o intervalo de tempo gasto para 68.000 metros cúbicos, com uma aproximação para 16 minutos, indicando a letra D como a alternativa correta:
Assim, fazemos as relações e simplificações para escrever "h" em função do tempo:
Podemos ampliar esse resultado para outra função, com o objetivo de indicar a altura da coluna de água na câmara em função do tempo. Para isso, deveremos considerar o valor inicial da altura da coluna (a partir dos vinte metros), sabendo que o nível descerá a cada minuto. Assim, construiremos uma função decrescente, com declividade negativa, indicada pela expressão h(t), que é a variação do nível construída anteriormente:
Essa função, descrita com uma declividade negativa de 21/17 metros por minuto, pode determinar a medida da coluna de água na câmara para qualquer intervalo de tempo. Vejamos o resultado para t = 6 minutos:
Mas ainda há outro aspecto importante para esse tipo de questão: ele envolve a unidade de volume. Trata-se de interpretarmos esse tipo de unidade, que pode ser aplicada em outros contextos.
Em nosso cotidiano, utilizamos o litro como unidade habitual e seria interessante compararmos a relação do volume de água que escoa na eclusa com o que consumimos diariamente. Para isso, vamos calcular quantos litros equivalem a um metro cúbico, lembrando que, quando se fala "um litro", subentende-se "um decímetro cúbico".
Como o decímetro é a décima parte do metro (ou, dizendo de outra forma, o metro é dez vezes o decímetro), construímos a relação entre as duas unidades de volume a partir dessa informação:
O volume da vazão, no escoamento de 4.200 metros cúbicos, pode ser transformado em litros, ficando 4.200 x 1000 = 4.200.000 litros por minuto.
Baseados em estimativas mundiais, os especialistas indicam que o ser humano adulto deve consumir, em média, 2 litros de água por dia, o que também causará vazão em alguma represa (uma vazão relacionada ao consumo e não à tecnologia aplicada para transportes de embarcações).
Agora, imagine uma cidade com uma população adulta igual a 7 milhões de habitantes, sendo que eles consomem, em média, 14 milhões de litros de água por dia (7 milhões x 2 litros de água por dia). Quantas vezes esse tipo de vazão é maior ou menor do que a vazão que ocorre na eclusa?
Na comparação dessas duas vazões não podemos nos esquecer de transformar as unidades de tempo na mesma base de cálculo. A opção é passar minuto para dia, ou dia para minuto, com as respectivas multiplicações para manter a proporção. Com esse procedimento, a vazão de água da eclusa é 432 vezes maior que o consumo de água na cidade do nosso exemplo. É o que mostra a resolução:
O primeiro passo para esse cálculo é identificar o volume de água no formato de um paralelepípedo com altura de 20 m, comprimento de 200 m e largura de 17 m:
 |
Como a vazão é de 4.200 metros cúbicos por minuto, com a regra de três calculamos o intervalo de tempo gasto para 68.000 metros cúbicos, com uma aproximação para 16 minutos, indicando a letra D como a alternativa correta:
 |
Observações
Uma abordagem interessante para este problema é calcular a variação do nível da água em função do tempo. Como já sabemos, a vazão (V) é a razão entre o volume da água no escoamento pelo respectivo tempo gasto, sendo que, para esta situação, as dimensões do volume serão de 17 m para a largura e 200 m para o comprimento, com a altura representada por "h", que indicará a variação do nível.Assim, fazemos as relações e simplificações para escrever "h" em função do tempo:
 |
Podemos ampliar esse resultado para outra função, com o objetivo de indicar a altura da coluna de água na câmara em função do tempo. Para isso, deveremos considerar o valor inicial da altura da coluna (a partir dos vinte metros), sabendo que o nível descerá a cada minuto. Assim, construiremos uma função decrescente, com declividade negativa, indicada pela expressão h(t), que é a variação do nível construída anteriormente:
 |
Essa função, descrita com uma declividade negativa de 21/17 metros por minuto, pode determinar a medida da coluna de água na câmara para qualquer intervalo de tempo. Vejamos o resultado para t = 6 minutos:
 |
Mas ainda há outro aspecto importante para esse tipo de questão: ele envolve a unidade de volume. Trata-se de interpretarmos esse tipo de unidade, que pode ser aplicada em outros contextos.
Em nosso cotidiano, utilizamos o litro como unidade habitual e seria interessante compararmos a relação do volume de água que escoa na eclusa com o que consumimos diariamente. Para isso, vamos calcular quantos litros equivalem a um metro cúbico, lembrando que, quando se fala "um litro", subentende-se "um decímetro cúbico".
Como o decímetro é a décima parte do metro (ou, dizendo de outra forma, o metro é dez vezes o decímetro), construímos a relação entre as duas unidades de volume a partir dessa informação:
 |
O volume da vazão, no escoamento de 4.200 metros cúbicos, pode ser transformado em litros, ficando 4.200 x 1000 = 4.200.000 litros por minuto.
Baseados em estimativas mundiais, os especialistas indicam que o ser humano adulto deve consumir, em média, 2 litros de água por dia, o que também causará vazão em alguma represa (uma vazão relacionada ao consumo e não à tecnologia aplicada para transportes de embarcações).
Agora, imagine uma cidade com uma população adulta igual a 7 milhões de habitantes, sendo que eles consomem, em média, 14 milhões de litros de água por dia (7 milhões x 2 litros de água por dia). Quantas vezes esse tipo de vazão é maior ou menor do que a vazão que ocorre na eclusa?
Na comparação dessas duas vazões não podemos nos esquecer de transformar as unidades de tempo na mesma base de cálculo. A opção é passar minuto para dia, ou dia para minuto, com as respectivas multiplicações para manter a proporção. Com esse procedimento, a vazão de água da eclusa é 432 vezes maior que o consumo de água na cidade do nosso exemplo. É o que mostra a resolução:
 |


Nenhum comentário:
Postar um comentário